Determine the Moment of Inertia of the Shaded Area
M Fundamentals of Structural ysis 2nd ed 2005. Click to see the answer Q.

Determine The Moment Of Inertia Of The Shaded Area About The X Axis Youtube
Web Moment Diagrams and Equations for Maximum Deflection.

. Calculate the moment of inertia of the section about its base a-a. Download Free PDF View PDF. Web The integral represented by Q is the first moment of the shaded area A with respect to the neutral axis z.
Web Transcribed Image Text. Since the pile cap is assumed perfectly rigid and all piles have the same area the pile reactions can be calculated based on the moment of inertia of the pile group as follows where Xi and Zi are the coordinates of a pile from the CG. Of the pile.
Oscar fabian gutierrez daza. Moment Diagrams and Equations for Maximum Deflection 5 6 Ezen Chi. The cross-sectional area of each member of the truss is 17 in2.
34a As in the case of a prismatic bar carrying a constant torque then. Determine the shear stress distribution in the section. The moment of inertia I about the NA is determined by the parallel axis theorem.
Assume b 11 in h 4 in r 2 in R 4 in. Determine the moment of inertia using the given x-axis of the shaded composite area and A. Download Free PDF View PDF.
Click to view larger image. The first moment is also used when calculating the value of shear stress at a particular point in the. La-a i R in.
Web Unlike the elastic section modulus S x the plastic section modulus has no fixed relationship to the moment of inertia of the cross section. Web Enter the email address you signed up with and well email you a reset link. Web Recognizing that is the polar moment of inertia of the cross-sectional area we can write this equation as G dθdx J T or 33 The rotation of the cross section at the free end of the shaft called the angle of twist θ is obtained by integration.
Web The pile group configuration plays an important role in the calculation of the pile reactions. Web If you compare the equations for Q above to the equations for calculating the centroid discussed in a previous section you will see that we actually use the first moment of area when calculating the centroidal location with respect to an origin of interest. The cross section of a bearing block is shown in the figure by the shaded area.
Rather it is defined as the sum of all elemental areas above or below the centroid x -axis of the cross section multiplied by the distance from each of the individual elemental centroids to the centroid of the cross.
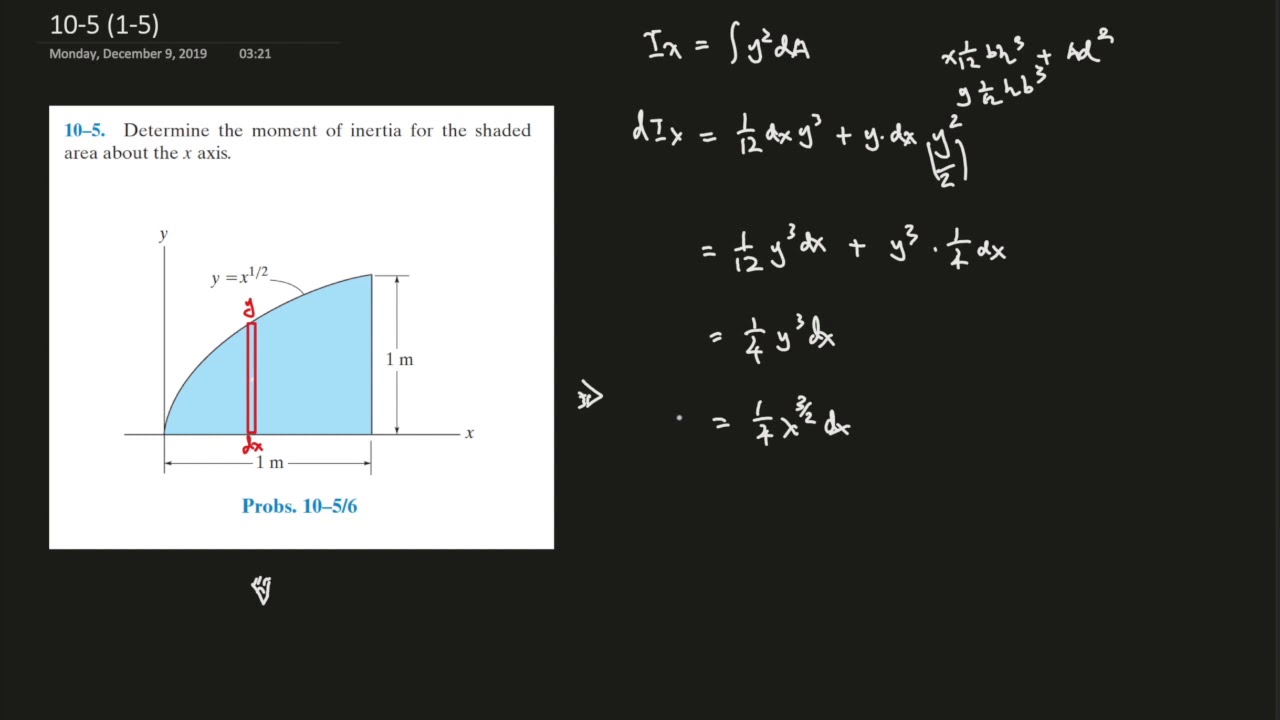
10 5 Determine The Moment Of Inertia For The Shaded Area About The X Axis Youtube

Determine The Moment Of Inertia Of The Shaded Area About The X Axis Youtube

10 6 Determine The Moment Of Inertia For The Shaded Area About The Y Axis Youtube

Statics 10 5 10 6 Determine The Moment Of Inertia For The Shaded Area About The X And Y Axis Youtube
0 Response to "Determine the Moment of Inertia of the Shaded Area"
Post a Comment